2017-05-14

したらばのスレをRのrvestを用いてスクレイピングする

Rにはrvestというスクレイピングする際のパッケージがある。
しかし、そのパッケージを用いて2chやしたらばなどのスレをスクレイピングをした記事は見当たらない。
（他の言語を用いてなされている記事もあるがhtmlに対して正規表現を用いて取り出しているのを見かけた）
http://qiita.com/murapon/items/5c7ec6568bc56799da99

今回は、スレッドのURLを与えた際にスレッドタイトルとレスの内容とレス日付を求めた。
以下にコードを示す。

library("rvest")
url<-"http://jbbs.shitaraba.net/bbs/read.cgi/study/9419/1481055888/" #shitaraba
html<-read_html(x=url)

#スレタイ
title_nodes<-html_nodes(html,"h1.thread-title")
thread_title<-html_text(title_nodes)

res_nodes<-html_nodes(html,"dd")
res<-html_text(res_nodes)
res<-gsub("\\n","",x=res)
res<-gsub(" ","",x=res)

res_date<-html_nodes(x = html,xpath='//*[@id="thread-body"]/dt')
res_date<-html_nodes(res_date,xpath='text()[3]')
res_date<-gsub("\\n","",x=res_date)
res_date<-gsub(" ","",x=res_date)
res_date<-gsub("：","",x=res_date)
res_date<-gsub("\\((月|火|水|木|金|土|日)\\)"," ",res_date)
res_POSIX<-as.POSIXlt(res_date)

今回は日付をPOSIX型に変換もやってみた。
（おそらく）後からあぼーんされてしまったレスがあるとそこがうまく取れないと思う。
次は2chでやる予定です。

2017-03-06

Mathematical Formulation of Bingo Probability and MonteCarlo Simulation(R)

This article is poor translation of my japanese articles.

There are a few papers related probability of Bingo games.

"A New Look at the Probabilities in Bingo"、Some Probability Problems Concerning the Game of Bingo

However, I cound not find a mathematical formulation of Bingo probability.

At first, I suppose there are $n \times n$ halls, max number $m$ (often 75), and number of calls $k$ .

For example, if we have $5 \times 5$ halls, there are 12 lines to bingo. I suppose probability of bingo in a line $p_{1}$ ,

$p_{1}=\frac{\dbinom{n}{n} \times \dbinom{m-n}{k-n}}{\dbinom{m}{k}}=\frac{\dbinom{m-n}{k-n}}{\dbinom{m}{k}}$

when there is no "FREE" hall.
This probability formulation is related to hypergeometric distribution.

Bingo happens in at least one of 12 lines, bingo probability $p$ is,
$p = 1-(1-p_{1})^{2 n + 2}$
.

In case there is free hall,
$p = 1-(1-p_{1})^{2 n - 2}(1-p_{2})^4$
where
$p_{2}=\frac{\dbinom{m-n+1}{k+1-n}}{\dbinom{m}{k}}$
.

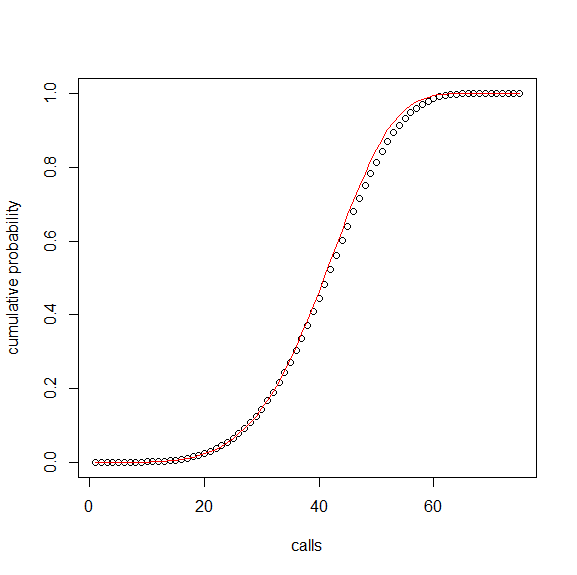
Figure shows a comparison MonteCarlo simulation and derived mathematical formulation, dotted points are simulation value and red line is derived one.

MonteCarlo simulation in 50000 times, $5 \times 5$ halls , and no "FREE" hall.

f:id:saikeisai:20170131013213p:plain

R simulation code below.

players<-50000
numrows <- numcols <- 5
maxNum <- 75
isfree <- TRUE # free : center

all_bingo<-list()
numBingoMatrix <- matrix(0,nrow=maxNum,ncol=players)

countBingo <- function(bingo,numrows){
#bingo bingo matrix
count <- 0
for(i in 1:numrows){
if(sum(bingo[,i])==0){
count <- count + 1
}
}
for(j in 1:numrows){
if(sum(bingo[j,])==0){
count <- count + 1
}
}

#antidiagonal
if(sum(diag(apply(bingo,2,rev)))==0){
count <- count + 1
}
if(sum(diag(bingo))==0){
count <- count + 1
}
return(count)
}

for(i in 1:players){
bingo<-matrix( (sample(1:maxNum,size = numrows*numcols,replace=FALSE)),ncol=numcols,nrow=numrows)
if(isfree){
bingo[(numcols+1)/2,(numrows+1)/2]<-0
}
all_bingo<-c(all_bingo,list(bingo))
}

skeleton <- all_bingo
calls <- sample(1:maxNum,size = maxNum,replace=FALSE)
bingoNum <- numeric(players)

for(j in 1:maxNum){
unlisted <- unlist(all_bingo)
unlisted[unlisted==calls[j]]<-0
all_bingo<-relist(flesh=unlisted,skeleton = skeleton)

for(k in 1:players){
bingoNum[k] <- countBingo(all_bingo[[k]],numrows)
}
numBingoMatrix[j,]<-bingoNum
}

temp <- numBingoMatrix>0
numberOfHit<-apply(temp,1,sum)


bingoProbability <- function(calls,maxNum,numrows,isfree){
p1 <- choose(maxNum-numrows,calls-numrows)/choose(maxNum,calls)
p2 <- p1
if(isfree){
p2 <- choose(maxNum-numrows+1,calls+1-numrows)/choose(maxNum,calls)
}
p <- 1-((1-p1)^(numrows*2-2))*((1-p2)^4)
return(p)
}


plot(numberOfHit/players,xlab="calls",ylab="cumulative probability")
lines(bingoProbability(calls=1:75,maxNum = 75,numrows=5,isfree=isfree),col=2)

2017-01-31

超幾何分布を利用してのビンゴの確率

前回saikeisai.hatenablog.comの続きです。

ビンゴの確率をちゃんと計算することを考えてみる。
まずは、 $n \times n$ のビンゴのマスとする。
最大の数を $m$ （75であることが多い）、呼ばれた番号の数を $k$ とする。
かんたんのために、まずはフリーマスなしで考える。
例えば、 $5 \times 5$ の場合は12本の線があるが、そのうちの一本でビンゴが起こる確率を $p_{1}$ とすると、
$p_{1}=\frac{\dbinom{n}{n} \times \dbinom{m-n}{k-n}}{\dbinom{m}{k}}=\frac{\dbinom{m-n}{k-n}}{\dbinom{m}{k}}$
となる。これは超幾何分布の確率っぽくなっている。
どれか一本の線でビンゴが起こればいいので、ビンゴが起こる確率を $p$ とすると、
$p = 1-(1-p_{1})^{2 n + 2}$
となる。
フリーマスがある場合には、
$p_{2}=\frac{\dbinom{m-n+1}{k+1-n}}{\dbinom{m}{k}}$
を用いて、
$p = 1-(1-p_{1})^{2 n - 2}(1-p_{2})^4$
となる。

この式を用いて、計算された確率を赤線、シミュレーションを5万回やったときの図を添付する。
条件は、 $5 \times 5$ のフリーマスありで最大75である。
f:id:saikeisai:20170131013213p:plain

まあ同じ・・かな？

以下、前回も載せたところもかぶるけどシミュレーションコード

players<-50000
numrows <- numcols <- 5
maxNum <- 75
isfree <- TRUE # free : center

all_bingo<-list()
numBingoMatrix <- matrix(0,nrow=maxNum,ncol=players)

countBingo <- function(bingo,numrows){
  #bingo bingo matrix
  count <- 0
  for(i in 1:numrows){
    if(sum(bingo[,i])==0){
      count <- count + 1
    }
  }
  for(j in 1:numrows){
    if(sum(bingo[j,])==0){
      count <- count + 1
    }
  }
  
  #antidiagonal
  if(sum(diag(apply(bingo,2,rev)))==0){
    count <- count + 1
  }
  if(sum(diag(bingo))==0){
    count <- count + 1
  }
  return(count)
}

for(i in 1:players){
  bingo<-matrix( (sample(1:maxNum,size = numrows*numcols,replace=FALSE)),ncol=numcols,nrow=numrows)
  if(isfree){
    bingo[(numcols+1)/2,(numrows+1)/2]<-0
  }
  all_bingo<-c(all_bingo,list(bingo))
}

skeleton <- all_bingo
calls <- sample(1:maxNum,size = maxNum,replace=FALSE)
bingoNum <- numeric(players)

for(j in 1:maxNum){
  unlisted <- unlist(all_bingo)
  unlisted[unlisted==calls[j]]<-0
  all_bingo<-relist(flesh=unlisted,skeleton = skeleton)
  
  for(k in 1:players){
    bingoNum[k] <- countBingo(all_bingo[[k]],numrows)
  }
  numBingoMatrix[j,]<-bingoNum
}

temp <- numBingoMatrix>0
numberOfHit<-apply(temp,1,sum)


bingoProbability <- function(calls,maxNum,numrows,isfree){
  p1 <- choose(maxNum-numrows,calls-numrows)/choose(maxNum,calls)
  p2 <- p1
  if(isfree){
    p2 <- choose(maxNum-numrows+1,calls+1-numrows)/choose(maxNum,calls)
  }
  p <- 1-((1-p1)^(numrows*2-2))*((1-p2)^4)
  return(p)
}


plot(numberOfHit/players,xlab="calls",ylab="cumulative probability")
lines(bingoProbability(calls=1:75,maxNum = 75,numrows=5,isfree=isfree),col=2)

2017-01-29

Rを用いてビンゴの確率について

ビンゴ（bingo）する確率について調べてみたけどあまりよくわからなかった。
とりあえず5×5でフリーマスありで、10000回（コードでは人数になってるけど）やってみた結果を添付します。
f:id:saikeisai:20170129184551p:plain

細かい結果を見てみると、mizutaの結果と少し異なり、
dinとほとんど同じ結果が得られた。
つまり、mizutaさんの式がどこか間違っているのだろうか。考えれば考えるほどわからなくなった。
論文では他に、"A New Look at the Probabilities in Bingo"、Some Probability Problems Concerning the Game of Bingoなど読んだ。

コード中では3×3や、4×4などを任意に変えられるようにしました。freeマスは4×4などでは上手く行かないかも。

以下コード

players<-10000
numrows <- numcols <- 5
maxNum <- 75
isfree <- TRUE # free : center

all_bingo<-list()
numBingoMatrix <- matrix(0,nrow=maxNum,ncol=players)

countBingo <- function(bingo,numrows){
  #bingo bingo matrix
  count <- 0
  for(i in 1:numrows){
    if(sum(bingo[,i])==0){
      count <- count + 1
    }
  }
  for(j in 1:numrows){
    if(sum(bingo[j,])==0){
      count <- count + 1
    }
  }
  
  #antidiagonal
  if(sum(diag(apply(bingo,2,rev)))==0){
    count <- count + 1
  }
  if(sum(diag(bingo))==0){
    count <- count + 1
  }
  return(count)
}

for(i in 1:players){
  bingo<-matrix( (sample(1:maxNum,size = numrows*numcols,replace=FALSE)),ncol=numcols,nrow=numrows)
  if(isfree){
    bingo[(numcols+1)/2,(numrows+1)/2]<-0
  }
  all_bingo<-c(all_bingo,list(bingo))
}

skeleton <- all_bingo
calls <- sample(1:maxNum,size = maxNum,replace=FALSE)
bingoNum <- numeric(players)

for(j in 1:maxNum){
  unlisted <- unlist(all_bingo)
  unlisted[unlisted==calls[j]]<-0
  all_bingo<-relist(flesh=unlisted,skeleton = skeleton)
  
  for(k in 1:players){
    bingoNum[k] <- countBingo(all_bingo[[k]],numrows)
  }
  numBingoMatrix[j,]<-bingoNum
}

temp <- numBingoMatrix>0
numberOfHit<-apply(temp,1,sum)
plot(numberOfHit/players,xlab="calls",ylab="cumulative probability")
numberOfHit/players